数据结构-串

📚 串的定义

基本概念

术语	描述
字符串	由0个或多个字符组成的有限序列，又称串
空串	长度为0的字符串（仍是合法子串）
主串	包含其他子串的字符串
子串	主串中任意连续字符组成的子序列

示例代码：

S = "IPhone 16 pro max"
S1 = "pro"  # S1是S的子串，空串也是S的子串

✨ 核心特性

1. 字符串是特殊的线性表，数据对象限定为字符集（如ASCII、Unicode）
2. 基本操作通常以子串为操作对象（非单个字符）

---

🎯 位置说明

概念	描述	示例
字符位置	字符在串中的序号（从1开始）	'h'在S中的位置为3
子串位置	子串首字符在主串中的位置	"one"在S中的位置为4

---

🗄️ 串的存储结构

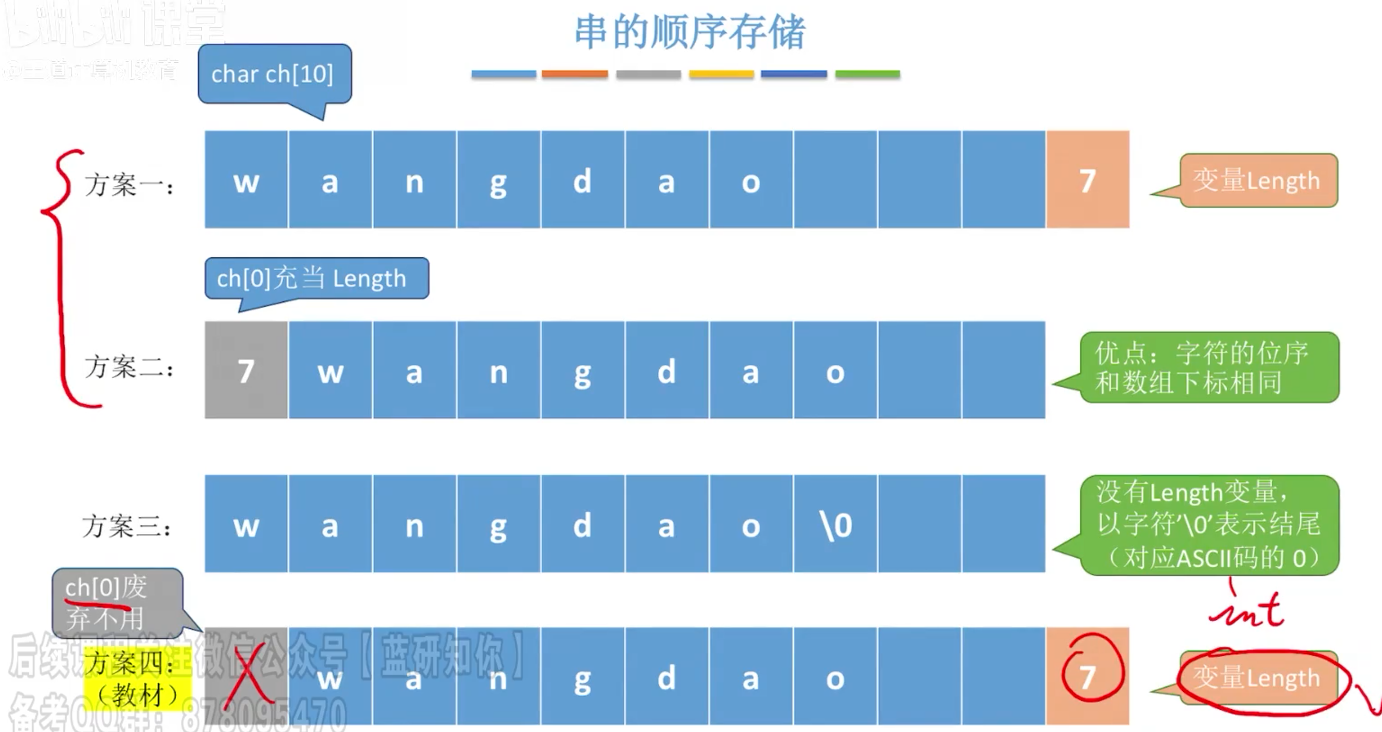
顺序存储

#define maxlen 20
typedef struct {
    char ch[maxlen];
    int length;
} SString;

链式存储

typedef struct StringNode {
    char ch;
    struct StringNode *next;
} StringNode, *String;

🔍 存储方案对比

顺序存储

• 优点：支持随机存取，存储密度大
• 缺点：扩展容量不方便，插入删除不方便

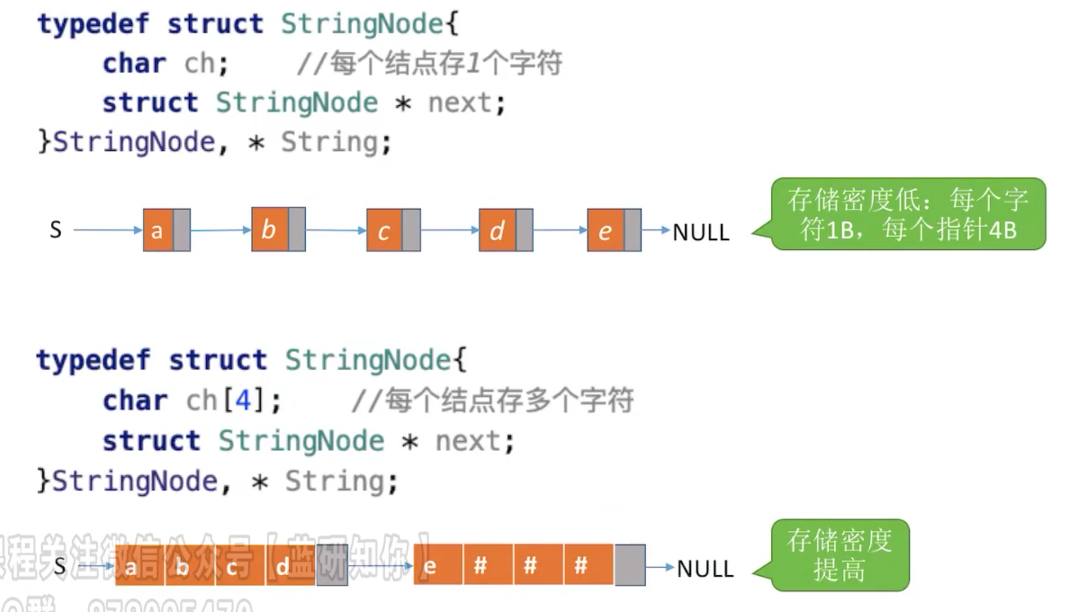
链式存储

• 优点：扩展容量分布，插入删除方便
• 缺点：不支持随机存取，指针占额外空间，存储密度小

---

🛠️ 串的基本操作

核心操作流程图

1. 求子串操作

SString SubString(SString S, int pos, int len) {
    SString sub;
    if (pos + len - 1 > S.length) {
        // 错误处理
    }
    for (int i = 0; i < len; i++) {
        sub.ch[i] = S.ch[pos + i - 1];
    }
    sub.length = len;
    return sub;
}

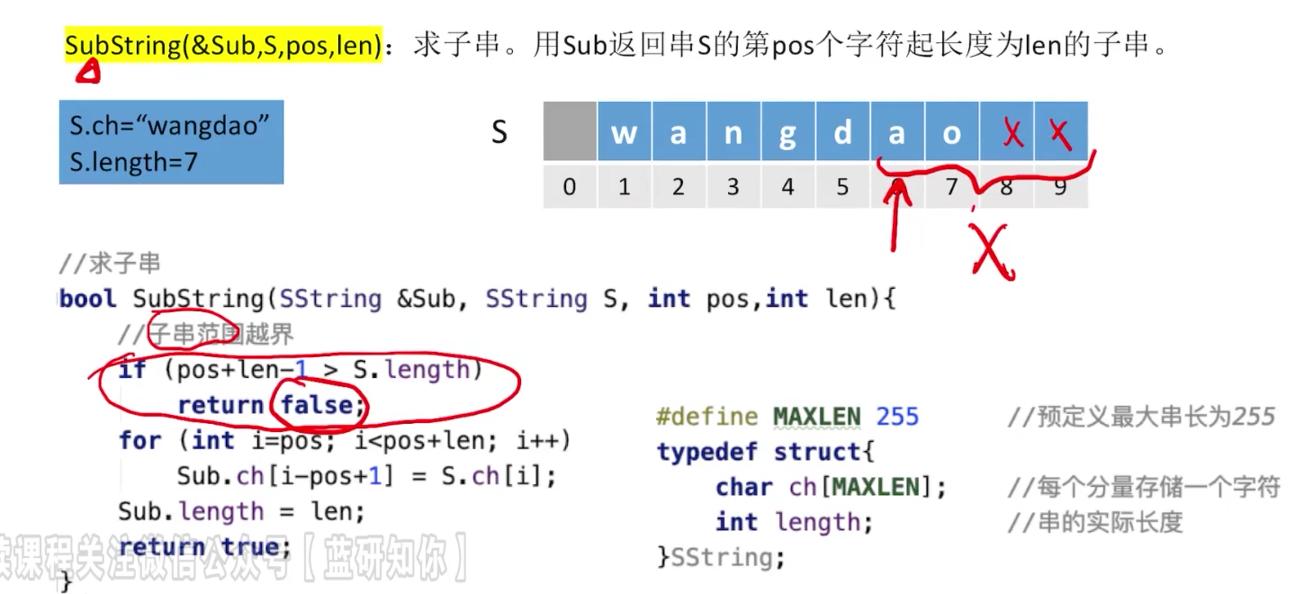
2. 字符串比较

3. 模式匹配

---

🔍 模式匹配算法

子串：主串的一部分，一定能在主串中找到
模式串：不一定能在主串中找到

朴素模式匹配

算法思想

• 主串S长度为n，模式串T长度为m
• 需要比较的次数为n-m+1
• 每次比较，i指向S，j指向T，i++，j++，依次匹配
• 如果遇到不匹配的字符
  • S需要从下一个位置开始，即i=i-j+2
  • T需要从头开始，即j=0
• 如果j>T.length，则表示匹配成功，返回i-T.length

时间复杂度分析

• 最佳情况，O(m)，第一次遍历成功
• 最差情况，O((n-m+1)*m)，每次都在最后一个字符匹配失败
• 平均情况，O(m+n)
• 空间复杂度，O(1)，只用固定数量的指针变量

---

🚀 KMP算法

由D.E.Knuth, J.H.Morris, V.R.Pratt提出，在朴素匹配算法的基础上改进

思路：

• 主串S，模式串T

• 当匹配到i个位置，发现不匹配

• 但主串S前面i-1个位置是匹配的，我们可以知道其具体内容

• 就可以选择某个位置进行下一次匹配，避免无效匹配

• 这个具体位置怎么表示，就是要探讨的内容

• 可以发现，到第i个位置不匹配，但主串前i-1个字符是已知的

• 主串不需要回溯，只需要模式串选择合适的位置j继续匹配

• 模式串指针和主串无关，只和自身有关

• 其值刚好可以用一个数组表示，表示为next[]

next数组构建：

void get_next(String T, int next[]) {
    int i = 1, j = 0;
    next[1] = 0;
    while (i < T.length) {
        if (j == 0 || T.ch[i] == T.ch[j]) {
            ++i; ++j;
            next[i] = j;
        } else {
            j = next[j];
        }
    }
}

KMP算法的实现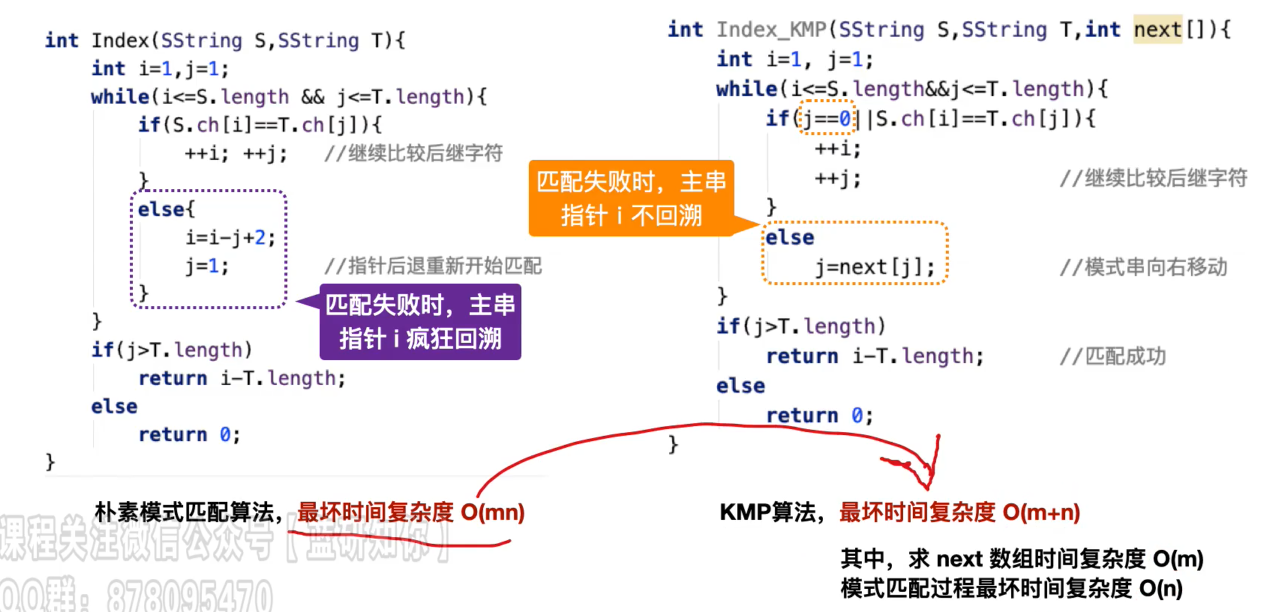

模式串’abaabc’的next数组：

j	1	2	3	4	5	6
next[j]	0	1	1	2	2	3

• 对于模式串’abaabc’
• 若第一个位置不匹配，令j=0， i++,j++再匹配
• 第二个，令j=1， i不变，继续匹配
• 第三个，令j=1， i不变，继续匹配
• 第四个，令j=2， i不变，继续匹配
• 第五个，令j=2， i不变，继续匹配
• 第六个，令j=3， i不变，继续匹配

---

⚡ KMP优化（nextval数组）

优化策略：

• 利用next数组匹配模式串时，当第i个字符不匹配，主串位置不变，模式串回到next[i]位置，此方法仅考虑前i-1个字符匹配情况

• 实际上，第i个字符不匹配，我们可以确定第i个字符一定不是m[i]，如果模式串回到next[i]位置，而该位置恰好为m[i]，这个匹配显然是多余的

• 在next数组的基础上，推出nextval数组，降低时间复杂度

void get_nextval(String T, int nextval[]) {
    int i = 1, j = 0;
    nextval[1] = 0;
    while (i < T.length) {
        if (j == 0 || T.ch[i] == T.ch[j]) {
            ++i; ++j;
            if (T.ch[i] != T.ch[j]) 
                nextval[i] = j;
            else 
                nextval[i] = nextval[j];
        } else {
            j = nextval[j];
        }
    }
}

算法思路

• nextval[1]一定为0
• 当T.ch[j]==T.ch[next[j]]，说明当前匹配是多余的，就算回到next[i]位置，依然不匹配
• nextval[j]=nextval[next[j]]
• 其余让nextval[j]=next[j]

---

📌 关键总结

1. 存储选择：顺序存储适合静态场景，链式存储适合动态场景
2. 模式匹配：KMP通过预处理将时间复杂度优化到O(n+m)
3. 算法优化：nextval数组避免重复无效匹配
4. 实践要点：注意字符串终止符’\0’的处理和长度校验